Envoyer un mail à l’auteur
xavier at ultra-fluide.com

Ressources

Combattre le spamdexing avec le TrustRank.

[Remarque : cette page nécessite un navigateur pourvu d'un moteur de rendu MathML pour visualiser les formules mathématiques.]

5 Sélection de l'échantillon initial

Le but de la fonction SelectSeed() est d'identifier les pages éligibles pour constituer l'échantillon initial. Nous souhaitons détecter les pages les plus utiles comme source de l'identification des autres bonnes pages. Dans le même temps nous voulons conserver un échantillon raisonnablement petit pour limiter l'appel à l'oracle. Dans ce chapitre nous proposons, au-delà d'une sélection purement aléatoire, deux autres stratégies pour définir la fonction SelectSeed().

5.1 PageRank inversé

fonction SelectSeed
input
     U    matrice de transition inverse
     N    nombre de pages
     αI   facteur d'amortissement 
     MI   nombre d'itérations
output
     s    score du PageRank inversé
begin 
     s = 1N 
     for i = 1 to M do  
             s = α·U·s+(1−α)·1N·1N
     return s
end

Figure 6 : Algorithme du PageRank inversé

Comme la confiance est distillée par les bonnes pages de l'échantillon source, l'une des approches est de donner la préférence aux pages permettant d'atteindre le plus grand nombre de pages, donc les pages comprenant de nombreux liens sortants. Dans la Figure 2 l'échantillon approprié si L=2 serait S={2,5} puisque les pages 2 et 5 offrent le plus grand nombre de liens (2 chacune).
Le raisonnement peut être étendu pour une meilleure couverture du graphe. Nous pouvons construire l'échantillon à partir de pages qui pointent vers de nombreuses pages qui elles mêmes pointent à nouveaux vers de nombreuses pages et ainsi de suite. Cette approche nous conduit à un modèle proche du PageRank, à la différence que le critère à optimiser repose sur le nombre de liens sortants au lieu du nombre de liens entrants. En conséquence le calcul de l'éligibilité d'une page peut être traité en appliquant le PageRank sur le graphe G'=(V,E') où :

(p,q) ∈E' ⇔(q, p) ∈ E

Les liens étant inversés, nous appelons notre algorithme PageRank inversé.
La Figure 6 montre la fonction SelectSeed basée sur le calcul du PageRank inversé. Notez que le facteur d'amortissement α I et le nombre d'itérations M I peuvent être différents des valeurs α B et M B utilisées pour l'algorithme du TrustRank. Le calcul est le même que celui du PageRank (chapitre 2.2), sauf que nous utilisons la matrice de transition inverse U à la place de la matrice de transition T.
Dans notre exemple Figure 2 l'algorithme du PageRank inversé ( α I = 0,85 et M I = 20) conduit au score suivant (résultat déjà donnés chapitre 4.3) :

s = [0.08, 0.13, 0.08, 0.10, 0.09, 0.06, 0.02]

Pour une valeur de L=3, l'échantillon de départ est S={2,4,5}. Les bonnes pages de l'échantillon sont dans l'ensemble S + ={2,4}, ce qui signifie que les pages 2 et 4 sont les points de départ pour la distribution des scores de confiance.

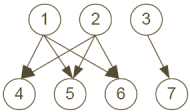
Figure 7: Un graphe pour lequel le PageRank inversé ne donne pas le maximum de couverture

Il est important de noter que le PageRank inversé est une heuristique (qui donne de bons résultats comme nous le verrons dans le chapitre 6). Tout d'abord le PageRank inversé ne garantit pas la couverture maximale. Par exemple, si l'on s'intéresse au graphe de la Figure 7 et pour L=2, la couverture maximale est obtenue avec l'échantillon {1,3} ou {2,3}. Cependant, le PageRank inversé conduit au vecteur suivant :

s = [0.05, 0.05, 0.04, 0.02, 0.02, 0.02, 0.02]

qui désigne l'échantillon {1,2}.
Le PageRank inversé reste cependant attractif car c'est un algorithme dont la complexité est polynomiale du nombre de pages, alors que déterminer le maximum de couverture est une complexité N-P .

Une seconde raison pour laquelle le PageRank inversé est une heuristique réside dans le fait que maximiser la couverture n'est pas systématiquement la meilleure stratégie. Pour illustrer, propageons la confiance par le fractionnement, sans avoir recours à l'atténuation. Prenant à nouveau la Figure 7, sélectionnons la page 2 comme échantillon et supposons que ce soit une bonne page. Les pages 4, 5 et 6 reçoivent chacune un score de 1/3. Prenons maintenant la page 3 pour échantillon et admettons qu'elle soit bonne également. Alors la page 7 aura un score de 1. Selon notre objectif, il est supérieur d'utiliser la page 3 puisque nous avons plus de certitude sur la page identifiée même si l'ensemble couvert est plus petit. D'un autre coté si nous utilisons des scores de confiance pour comparaison à d'autres scores de confiance il sera certainement préférable de qualifier un plus grand nombre de pages en acceptant une moindre précision.

5.2 PageRank élevé

Nous avons considéré jusqu'à présent que l'identification d'une page en tant que bonne ou mauvaise page avait une valeur identique pour toutes les pages web. Pourtant il est certainement plus intéressant de s'assurer de la qualité de pages qui apparaissent en premier dans les résultats de recherche. Prenons par exemple 4 pages p, q, r, et s dont le contenu correspond de façon équivalente à une recherche donnée. Si le moteur de recherche utilise le PageRank pour ordonner ses résultats, la page présentant le meilleur PageRank, disons p, sera placée en tête, puis la page q si son PageRank arrive en deuxième, et ainsi de suite. Comme il est vraisemblable que l'utilisateur s'intéresse d'abord aux pages p et q plutôt qu'à r et s (qui ne seront peut-être même pas vues si elles sont sur les pages de résultats suivantes), il semble plus utile d'obtenir une bonne précision sur les pages p et q. Si la page p utilise le spamdexing, l'utilisateur devrait plutôt visiter q à la place.
Ainsi une seconde heuristique pour établir l'échantillon de départ serait de donner préférence aux pages de fort PageRank. Comme les pages de fort PageRank ont de bonnes chances de pointer sur des pages de fort PageRank également, les scores de confiance vont se propager aux pages qui ont de fortes probabilités d'être en début de résultats de recherche. Sélectionnant l'échantillon de départ avec le PageRank nous identifierions certainement la qualité d'un plus petit nombre de pages qu'avec le PageRank inversé, mais cette qualification toucherait les pages dont il est particulièrement important de connaître le niveau de confiance.

Agence de communication Ultra-Fluide : 01 47 70 23 32 - contact at ultra-fluide.com - 44 rue Richer 75009 Paris.