Envoyer un mail à l’auteur
xavier at ultra-fluide.com

Ressources

• Marquage sémantique XSLT
• CSS
• XHTML
• Extensions Firefox
• TrustRank, anti-spam
  • Introduction
  • Préliminaires
  • Fonction de confiance
  • Amortissement de la confiance
  • Echantillon initial
  • Résultats
  • Conclusion
• Datamining
• Divers web

Combattre le spamdexing avec le TrustRank.

[Remarque : cette page nécessite un navigateur pourvu d'un moteur de rendu MathML pour visualiser les formules mathématiques.]

3 Evaluation de la confiance

3.1 Fonction Oracle et fonction de Confiance

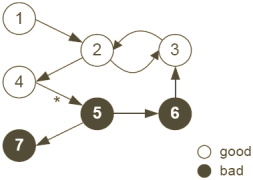
Figure 2: Univers web constitué de bonnes et mauvaises pages.

Comme expliqué dans le premier chapitre, juger du spamdexing nécessite une évaluation humaine. Nous allons formaliser la notion du contrôle humain par une fonction binaire, la fonction Oracle définie sur l'ensemble des pages p∈V :

$O\left(p\right)=\{\begin{array}{cc}0\hfill & \text{si }p\text{ est bonne}\hfill \\ 1\hfill & \text{si }p\text{ est du spamdexing}\hfill \end{array}$

La Figure 2 présente un univers web de sept pages ou les bonnes pages sont en blanc et le spamdexing en noir. L'appel de la fonction Oracle sur les pages 1 à 4 retourne la valeur 1.

Les invocations de l'Oracle sont coûteuses en temps et en argent. Nous ne souhaitons donc pas appeler cette fonction pour toutes les pages. Notre objectif est de rester sélectif, c'est à dire de demander à l'expert humain son évaluation sur certaines pages seulement.

Pour déterminer les bonnes pages sans invoquer l'Oracle sur tout le web, nous nous reposerons sur un constat empirique essentiel que nous appellerons "isolation approximative" des bonnes pages : les bonnes pages pointent rarement vers les mauvaises. Cette propriété est assez intuitive car les pages utilisant le spamdexing sont réalisées pour tromper les moteurs de recherche, et pas pour présenter de l'information utile. Il en résulte que les personnes créant de bonnes pages n'ont que peu de raisons de les lier aux mauvais contenus.

Cependant les créateurs de bonnes pages peuvent parfois être abusés, et nous trouvons de temps en temps des liens de bonnes à mauvaises pages (page 4 vers pages 5 marqué d'un astérisque sur la Figure 2). Considérons l'exemple suivant. Supposons l'existence d'un forum de bonne qualité mais non modéré, les spammers pourront y inclure via des messages innocents des URLs vers leurs pages. Il en résulte que de bonnes pages vont pointer vers des mauvaises. Un autre cas de figure est celui des pots de miel : un site utilisant le spamdexing propose des ressources dignes d'intérêt (une documentation Unix par exemple) qui renferment des liens cachés vers les mauvaises pages. Le pot de miel attire des liens à lui pour amplifier le classement de la zone de spam.

Notons que la réciproque du principe d'isolation approximative n'a pas cours : les pages spammées peuvent, et dans la pratique sont souvent reliées à de bonnes pages. Les spammers pointent sur de bonnes pages soit pour créer un pot de miel soit dans l'espoir que de bons liens externes vont augmenter le classement de leur plate-forme [10].

Pour évaluer les pages sans se reposer sur l'Oracle, nous devons estimer la vraisemblance qu'une page donnée soit bonne. Plus formellement nous définissons la "fonction de confiance" T produisant des valeurs dans l'intervalle 0 (mauvais), 1 (bon). Idéalement pour chaque page p, T(p) devrait donner la probabilité que la page p soit bonne :

Fonction de confiance idéale

T(p) = Pr[O(p) = 1]

Pour illustrer, considérons un ensemble de 100 pages et disons que le score de la fonction de confiance soit pour chaque page de 0,7. Supposons également que nous évaluons chacune des 100 pages avec la fonction Oracle. Si T est correcte, la fonction Oracle devrait donner 1 pour 70 pages et 0 pour les 30 restantes.

Dans la pratique il est très difficile d'obtenir une telle fonction T. Néanmoins, même si T ne mesure pas précisément la vraisemblance qu'une page est bonne, une fonction capable d'ordonner les pages selon ce critère de vraisemblance nous serait déjà utile. Ainsi lorsqu'une paire de page p et q sera telle que le score de confiance de p est inférieur à celui de q, cela devrait indiquer que q a plus de chance d'être bonne que p. Cette fonction permettrait au moins d'ordonner les résultats de recherche en donnant la préférence aux pages ayant une probabilité supérieure d'être bonne. Formellement, la propriété souhaitable pour la fonction de confiance s'écrit :

Fonction de confiance ordonnée

T(p) < T(q) ⇔ Pr[O(p) = 1] < Pr[O(q) = 1]
T(p) = T(q) ⇔ Pr[O(p) = 1] = Pr[O(q) = 1]

Une autre façon de relâcher les exigences sur T est d'introduire le seuil δ :

Fonction de confiance à seuil

T(p) > δ ⇔ O(p) = 1

Si une page p reçoit un score supérieur à δ, nous savons qu'elle est bonne, et sinon nous ne pouvons rien décider sur p. Une telle fonction T sera capable de dire qu'un sous ensemble de pages recevant un score au-delà de δ sera bon. Notons cependant que cette fonction T de confiance à seuil ne permet pas nécessairement d'ordonner les pages selon leur probabilité d'être bonne.

3.2 Métriques d'évaluation

Ce chapitre introduit trois métriques qui nous aiderons à évaluer si une fonction T donnée satisfait les conditions souhaitées.
Nous supposons disposer un ensemble X de pages web sur lesquelles il sera possible d'invoquer T et O. Nous pourrons ensuite déterminer si une propriété souhaitée est atteinte sur cet ensemble. Dans le chapitre 6 nous discuterons le moyen de sélectionner un ensemble X significatif, mais pour l'instant supposons simplement que c'est un ensemble de pages pris au hasard.
Notre première métrique dite des paires ordonnées, est liée à la fonction de confiance ordonnée. Nous introduisons une fonction booléenne I(T,O,p,q) qui indique si une mauvaise page reçoit un score supérieur ou égal à celui d'une bonne page. (violation de la fonction de confiance ordonnée) :

$I(T,O,p,q)=\{\begin{array}{cc}1\hfill & \hfill \text{si }T\left(p\right)\ge T\left(q\right)\mathrm{ et }O\left(p\right)<O\left(q\right),\hfill \\ 1\hfill & \hfill \text{si }T\left(p\right)\le T\left(q\right)\mathrm{ et }O\left(p\right)>O\left(q\right),\hfill \\ 0\hfill & \text{sinon.}\hfill \end{array}$

Ensuite nous générons de notre ensemble X un ensemble P de paires ordonnées (p,q), p≠q, puis nous calculons la fraction de paires pour lesquelles T ne se trompe pas :

métrique des paires ordonnées

$\mathrm{pairord}(T,O,P)=\frac{\mid P\mid -{\sum }_{(p,q)\in P}\mathrm{ I}(T,O,p,q)}{\mid P\mid }$

Pairord vaut 1 lorsque T classe correctement l'ensemble des pages. Au contraire lorsque pairord vaut 0, T ne classe aucune des paires de pages correctement. Dans le chapitre 6 nous expliquons la façon de sélectionner un ensemble P de paires pour l'évaluation.
Nos deux autres métriques sont relatives à la fonction de confiance à seuil. Les métriques classiques de précision et rappel [1] sont les fonctions auxquelles il est naturel de penser pour la mesure de la performance de la fonction T associée à un seuil δ donné. Nous définissons la précision comme la fraction du nombre des bonnes pages parmi celles ayant un score supérieur à δ.

Précision

$\mathrm{prec}(T,O)=\frac{\mid \{p\in X/T(p)>\mathrm{\delta and }O(p)=1\}\mid }{\mid \{q\in X/T(q)>\delta \}\mid }$

Dans la même optique nous définissons le rappel comme la fraction du nombre de pages ayant un score supérieur à δ parmi les bonnes pages.

Rappel

$\mathrm{rec}(T,O)=\frac{\mid \{p\in X/T(p)>\mathrm{\delta and }O(p)=1\}\mid }{\mid \{q\in X/O(q)=1\}\mid }$