Envoyer un mail à l’auteur
xavier at ultra-fluide.com

Combattre le spamdexing avec le TrustRank.

[Remarque : cette page nécessite un navigateur pourvu d'un moteur de rendu MathML pour visualiser les formules mathématiques.]

4 Calcul de la confiance

Commençons notre recherche d'une fonction de confiance fiable par des approches simples. Ensuite nous combinerons les observations rassemblées pour construire un l'algorithme du TrustRank au chapitre 4.3.
Soit un budget limité L du nombre d'invocation de la fonction Oracle, nous prenons au hasard un échantillon S de L pages et leur appliquons la fonction oracle (nous verrons dans le chapitre 5 un moyen d'améliorer l'échantillon). Nous appelons les sous ensembles des bonnes et mauvaises pages respectivement $S^{+}$ et $S^{-}$ . Comme les autres pages ne sont pas contrôlées par un humain, nous leur assignons un niveau de confiance à 1/2 pour indiquer notre manque d'information. En conséquence nous appelons cette fonction initiale $T_{0}$ la fonction de confiance ignorante, définie pour tout p ∈ V :

Fonction de confiance ignorante 



 $T_{0} (p) = {\begin{matrix} O (p) & si p ∈S \\ 1 / 2 & sinon \end{matrix}$

Par exemple, nous pouvons fixer L à 3 dans le contexte proposé par la Figure 2. Un échantillon pris par hasard pourrait être S={1,3,6}. Soit o et $t_{0}$ respectivement les vecteurs de l'oracle et de la fonction de confiance. Dans ce cas :

o = [1, 1, 1, 1, 0, 0, 0]

 $t_{0} = [1, \frac{1}{2}, 1, \frac{1}{2}, \frac{1}{2}, 0, \frac{1}{2}]$

Pour évaluer les performances de la fonction de confiance ignorante, supposons que notre ensemble X est constitué des 7 pages de la Figure 2, ceci nous conduit à 42=7x6 paires ordonnées. Dans ce cas la métrique pairord() pour la fonction de confiance ignorante $T_{0}$ est de 17/21. La précision est de 1 et le rappel de 1/2 pour un seuil de δ=1/2.

4.1 Propagation de la confiance

Pour notre prochaine étape, nous tirons avantage du principe d'isolation approximative des bonnes pages. Nous prenons par hasard l'ensemble S de L pages que nous soumettons à l'oracle. Supposant que les bonnes pages pointent sur d'autres bonnes pages, nous affectons un score de 1 à toutes les pages qui peuvent être atteintes à partir d'une page de $S^{+}$ en M étapes ou moins. La fonction de confiance correspondante $T_{M}$ a les caractéristiques suivantes :

M	pairord	prec	rec
1	19/21	1	3/4
2	1	1	1
3	17/21	4/5	1

Tableau 1 : performance de la fonction de confiance $T_{M}$ pour M∈{1,2,3}

Fonction de confiance à M étapes



 $T_{M} (p) = {\begin{matrix} 1 & si p \in S, \\ 1 & si p \notin S et \exists q \in S^{+} /q ⇝_{M} p \\ 1 / 2 & sinon. \end{matrix}$

Où q $⇝_{M} p$ indique l'existence d'un chemin de navigation de M étapes de la page q vers la page p sans qu'aucune des étapes ne soit une mauvaise page.
Reprenant l'exemple de la Figure 2, et l'échantillon S={1,3,6}, les 3 premières fonctions de confiance sont :

 ${M = 1 : t}_{1} = [1, 1, 1, \frac{1}{2}, \frac{1}{2}, 0, \frac{1}{2}]$ 

 ${M = 2 : t}_{2} = [1, 1, 1, 1, \frac{1}{2}, 0, \frac{1}{2}]$ 

 ${M = 3 : t}_{3} = [1, 1, 1, 1, 1, 0, \frac{1}{2}]$

Nous souhaiterions que $T_{M}$ obtienne de meilleures performances que $T_{0}$ au regard de l'une de nos métriques. Effectivement le tableau 1 montre que pour M=1 et M=2 les métriques des paires ordonnées et de rappel augmente, tandis que la précision reste à 1. Cependant les résultats sont moins bons avec M=3. La raison en est que la page 5 reçoit un score de 1 du fait du lien reçu de la page 4 (lien marqué d'un astérisque sur la Figure 2).
Comme nous venons de le voir, la fonction de confiance à M étapes pose un problème puisque nous ne sommes pas totalement certains que toutes les pages reliées à notre échantillon de bonnes pages soient bonnes également. En fait, plus la distance à notre échantillon de bonnes pages est grande plus la probabilité de tomber sur une bonne page baisse. Dans la Figure 2 il y a 2 pages (pages 2 et 4) reliées au plus à 2 étapes de l'échantillon de bonnes pages. Comme ces 2 pages sont bonnes, la probabilité d'atteindre une bonne page en 2 étapes au plus est de 1. Par contre 3 pages peuvent être atteintes en 3 étapes au plus, mais 2 seulement sont bonnes (pages 2 et 4), alors que la troisième, la page 5 est mauvaise. Donc la probabilité d'atteindre une bonne page en 3 étapes au plus tombe à 2/3.

4.2 Amortissement de la confiance

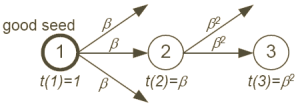
Figure 3: Confiance atténuée

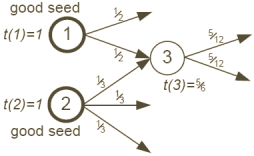
Figure 4: Confiance fractionnée

Ces observations suggèrent que nous devrions diminuer la confiance à mesure que nous prenons de la distance avec l'échantillon de bonnes pages. Il y a bien des façons d'envisager l'amortissement de la confiance, nous en décrirons deux possibles.
La Figure 3 illustre la première idée que nous appellerons confiance atténuée. Comme la page 2 est à une étape de l'échantillon de bonnes pages grâce à la page 1, nous lui affectons un score de confiance amorti de β, avec β<1. Comme la page 3 est à un lien de la page 2 dont le score est β, nous affectons à cette page 3 un score amorti de βxβ. Nous avons également besoin de définir l'affectation de la confiance dans le cas de liens entrants multiples. Par exemple, supposons toujours dans le cadre de la Figure 3, que la page 1 pointe également vers la page 3. Nous pourrions alors affecter à la page 3 le score de confiance le plus élevé c'est à dire β, ou alors un score moyen, c'est à dire (β+βxβ)/2.
La seconde méthode proposée pour l'amortissement de la confiance est appellée confiance fractionnée et repose sur le constat suivant : le soin apporté à ajouter des liens sur une page est souvent inversement proportionnel au nombre de liens présents sur la page. En d'autres termes, si une bonne page n'a qu'une poignée de liens sortants, alors il est vraisemblable que les pages ciblées soient bonnes également. Au contraire une bonne page contenant des centaines de liens sortants a une probabilité plus élevée de pointer vers des mauvaises pages.
Cette observation nous conduit à fractionner la confiance lors de la propagation aux autres pages : si une page p a niveau de confiance de T(p) et pointe vers ω(p) pages, alors chacune des ω(p) pages va recevoir une fraction T(p)/ω(p) de la confiance de p. Dans ce cas la confiance d'une page sera la somme des fractions reçues de tous ses liens entrants. Intuitivement, plus une page accumule de crédit provenant des pages environnantes, plus il y a de chance qu'elle soit bonne. (nous pouvons bien sur normaliser la somme pour que la confiance reste dans l'intervalle [0,1]).
La Figure 4 illustre ce fractionnement de la confiance. La page 1 élément de l'échantillon de bonnes pages a 2 liens sortants et distribue donc la moitié de son score de confiance à chacune de ses cibles. De façon similaire la page 3 distribue le tiers de son score de confiance. Le score de la page 3 sera donc de 1/2+1/3=5/6.
Notons que nous pouvons associer les deux techniques d'atténuation et de fractionnement. Dans ce cas la page 3 recevra un score de βx(1/2+1/3).
Il y a de multiples façons d'implémenter la confiance atténuée et/ou fractionnée. Dans le chapitre suivant nous présentons une formulation qui s'inspire du calcul du PageRank biaisé en M étapes. Cette caractéristique signifie que l'on peut se reposer sur le code de l'algorithme du PageRank (avec quelques changements mineurs) pour calculer les scores de confiance. C'est un avantage important puisque que de substantiels efforts ont déjà été consentis pour optimiser ce calcul sur de très grands ensembles de données (voir par exemple [5,8]).

4.3 Algorithme du TrustRank

fonction TrustRank
input
     T    matrice de transition
     N    nombre de pages
     L    nombre maximum d'invocations de la fonction oracle
      $α_{B}$    facteur de décroissante pour le PageRank biaisé
      $M_{B}$    nombre d'itération pour le PageRank biaisé
output
      $t^{*}$    TrustRank scores
begin
     // désignation des pages éligibles à l'échantillon
(1)  s  SelectSeed(...)
     // classement correspondant
(2)  σ = Rank({1,...,N},s)
     // selection des bonnes pages dans l'échantillon
(3)  d =  $0_{N}$ 
     for i = 1 to L do  
             if O(σ(i)) == 1 then 
		d(σ(i)) = 1
     // normalisation de la composante statique de la confiance
(4)  d = d/|d|
     // calcul du TrustRank
(5)   $t^{*}$ = d
     for i = 1 to  $M_{B}$  do
              $t^{*}$ =  $α_{B}$ ·T· $t^{*}$ +(1- $α_{B}$ )·d
     return
end

Figure 5 : Algorithme de calcul du TrustRank

La fonction TrustRank de la Figure 5 calcul la fonction de confiance pour un graphe web. Nous allons expliquer son fonctionnement au travers son exécution sur le graphe de la Figure 2.
L'algorithme admet en entrée le graphe web (matrice de transition T et nombre N de pages web) et les paramètres de contrôle de l'exécution (L, $M_{B}$ , $α_{B}$ , voir ci-dessous).
Dans la première étape, l'algorithme appelle la fonction SelectSeed() qui retourne un vecteur s. La coordonnée s(p) de ce vecteur exprime le degré d'éligibilité de la page p à faire partie de l'échantillon. (voir le chapitre 5 pour plus de détails). Comme nous le verrons au chapitre 5.1, l'une des versions de la fonction SelectSeed() appliquée à la Figure 2 retourne le vecteur suivant :

s = [0.08, 0.13, 0.08, 0.10, 0.09, 0.06, 0.02]

Dans l'étape (2) la fonction Rank(x, s) génère une permutation x' du vecteur x avec les coordonnées x'(i) rangées en ordre décroissant de s(x'(i)). En d'autres termes, la fonction Rank() réordonne les coordonnées de x en ordre décroissant des scores obtenus avec la fonction SelectSeed(). Dans notre exemple, nous avons :

σ = [2, 4, 5, 1, 3, 6, 7]

Cela signifie que la page 2 est la mieux placée pour entrer dans l'échantillon, puis la page 4, etc.

Lors de l'étape (3) nous appelons la fonction oracle sur les L pages les mieux placées pour entrer dans l'échantillon. Les pages de la composante statique de la distribution de confiance (coordonnées du vecteur d) qui correspondent à de bonnes pages obtiennent un score de 1.

Enfin, l'étape (5) évalue le TrustRank selon le calcul du PageRank biaisé avec d en remplacement de la distribution uniforme. A noter que l'étape (5) implémente une version particulière de la confiance atténuée et fractionnée. A chaque itération la confiance d'une page est fractionnée pour être distribuée sur ses voisins et atténuée avec un coefficient $α_{B}$ . En choisissant $α_{B}$ = 0,85 et $M_{B}$ = 20, l'algorithme conduit au résultat suivant :

$t^{*}$ = [0, 0.18, 0.12, 0.15, 0.13, 0.05, 0.05]

Compte tenu du fait que la confiance se propage par itération, les bonnes pages de l'échantillon (pages 2 et 4) ne maintiennent pas leur score à 1. Elles se retrouvent cependant avec les plus hauts scores. A noter également que la bonne page 4 de l'échantillon reçoit un score inférieur à son homologue la page 2. Ceci est dû à la structure des liens : la page 2 bénéficie d'un lien entrant de la part d'une page disposant d'un bon score (page 3), ce qui n'est pas le cas de la page 4. L'algorithme de TrustRank "raffine" le score donné par l'oracle en classant les bonnes pages, indiquant que la page 2 a finalement plus de chance d'être bonne que la page 4. Il est possible par ailleurs de normaliser le résultat en divisant tous les scores par le score le plus élevé (le score de la page 2 devenant égale à 1), mais cette opération ne change pas le classement des pages.
Nous voyons avec cet exemple que le TrustRank affecte globalement des scores plus hauts aux bonnes pages qu'aux autres. En particulier 3 des 4 bonnes pages (pages 2, 3 et 4) obtiennent de bons scores alors que 2 des 3 mauvaises pages (pages 6 et 7) obtiennent de faibles scores. Cependant l'algorithme échoue sur les pages 1 et 5. La page 1 n'était pas dans l'échantillon de départ et n'a aucun lien entrant lui permettant d'obtenir par propagation un score de confiance différent de 0. Toutes les bonnes pages sans référence subiront le même sort à moins d'être sélectionnées dans l'échantillon initial. La mauvaise page 5 reçoit un bon score de confiance puisqu'elle est la cible d'un de ces rares liens de bonne à mauvaise page. Comme nous le verrons au chapitre 6, en dépit d'erreurs comme celles-ci, l'algorithme TrustRank reste tout de même capable d'identifier une proportion significative de bonnes pages.

Agence Communication, Web et Technologies

Combattre le spamdexing avec le TrustRank.

4 Calcul de la confiance

4.1 Propagation de la confiance

4.2 Amortissement de la confiance

4.3 Algorithme du TrustRank